Direct variation is a concept that pops up in all sorts of everyday situations, whether you're cooking, shopping, or even planning a road trip. It’s essentially about how two things are connected in a way where one grows or shrinks as the other does. For example, if you double the amount of sugar in a recipe, the sweetness increases proportionally. This idea is what we’ll explore today, breaking it down into easy-to-digest pieces so you can understand how direct variation works and why it matters.
When we talk about direct variation, we’re referring to a special kind of relationship between two variables. Think of it like this: if one variable increases, the other does too, and if one decreases, the other follows suit. This concept isn’t just useful in math class—it applies to real-life scenarios like calculating how much you’ll earn based on hours worked or figuring out how far you can drive with a certain amount of gas. By the end of this article, you’ll have a solid grasp of direct variation and how it plays out in the world around you.
Now, let’s dive right into the heart of the matter. Direct variation is more than just a math term—it’s a practical tool that helps us make sense of the world. Whether you’re a student trying to ace algebra or someone curious about how numbers interact, this guide will walk you through everything you need to know. From defining what direct variation is to seeing it in action through examples, we’ll cover all the bases. So, let’s get started!
Table of Contents
- What Exactly is Direct Variation?
- Why Does Direct Variation Matter?
- Can You Identify Direct Variation in Real Life?
- How Do You Write the Equation for Direct Variation?
- What Does the Graph of Direct Variation Look Like?
- Is Direct Variation Always a Straight Line?
- How Can You Solve Direct Variation Problems?
- Wrapping Up - What Have We Learned About Direct Variation?
What Exactly is Direct Variation?
Alright, let’s break it down. Direct variation is a fancy way of saying that two things change together in a predictable way. If one goes up, the other goes up, and if one goes down, the other follows suit. In math terms, we express this as y = kx, where k is the constant of proportionality. This constant tells us how much y changes for every unit of x.
So, what does this mean in real life? Imagine you’re filling up a water balloon. The more water you add, the bigger the balloon gets. The size of the balloon varies directly with the amount of water you pour in. It’s a simple idea, but it’s incredibly powerful when you start applying it to more complex situations.
Can You Identify Direct Variation in Real Life?
Direct variation shows up in all sorts of places. For instance, when you’re driving, the distance you travel varies directly with the time you spend on the road. If you double the time, you’ll cover twice the distance, assuming you maintain the same speed. Similarly, if you’re baking, doubling the recipe means doubling the ingredients. These are just a couple of examples, but there are countless others.
In some respects, direct variation is like a seesaw. When one side goes up, the other does too. It’s a relationship that’s straightforward and easy to spot once you know what to look for. So, next time you’re out and about, try to spot examples of direct variation in action. You might be surprised at how often it comes up!
Why Does Direct Variation Matter?
Direct variation isn’t just a theoretical concept—it has real-world applications that affect our daily lives. For example, businesses use it to predict sales based on advertising spend. If they spend twice as much on ads, they expect to see twice the sales. Engineers use it to calculate how much material they’ll need for a project. Even something as simple as calculating your weekly grocery bill can involve direct variation.
Sometimes, it’s almost hard to believe how much direct variation impacts our lives. It’s not just about math class—it’s about making sense of the world and predicting outcomes. Whether you’re a student, a professional, or just someone curious about how things work, understanding direct variation can give you a new perspective on the relationships between different factors.
How Do You Write the Equation for Direct Variation?
Writing the equation for direct variation is simpler than you might think. All you need is the formula y = kx. Here, y represents one variable, x represents the other, and k is the constant of proportionality. This constant tells you how much y changes for every unit of x. For example, if k is 3, then y will be three times x.
Let’s look at a quick example. Suppose you’re buying apples, and each apple costs $1. If you buy 5 apples, you’ll spend $5. In this case, the cost (y) varies directly with the number of apples (x), and the constant of proportionality (k) is 1. So, the equation would be y = 1x, or simply y = x. See? It’s not so complicated after all.
What Does the Graph of Direct Variation Look Like?
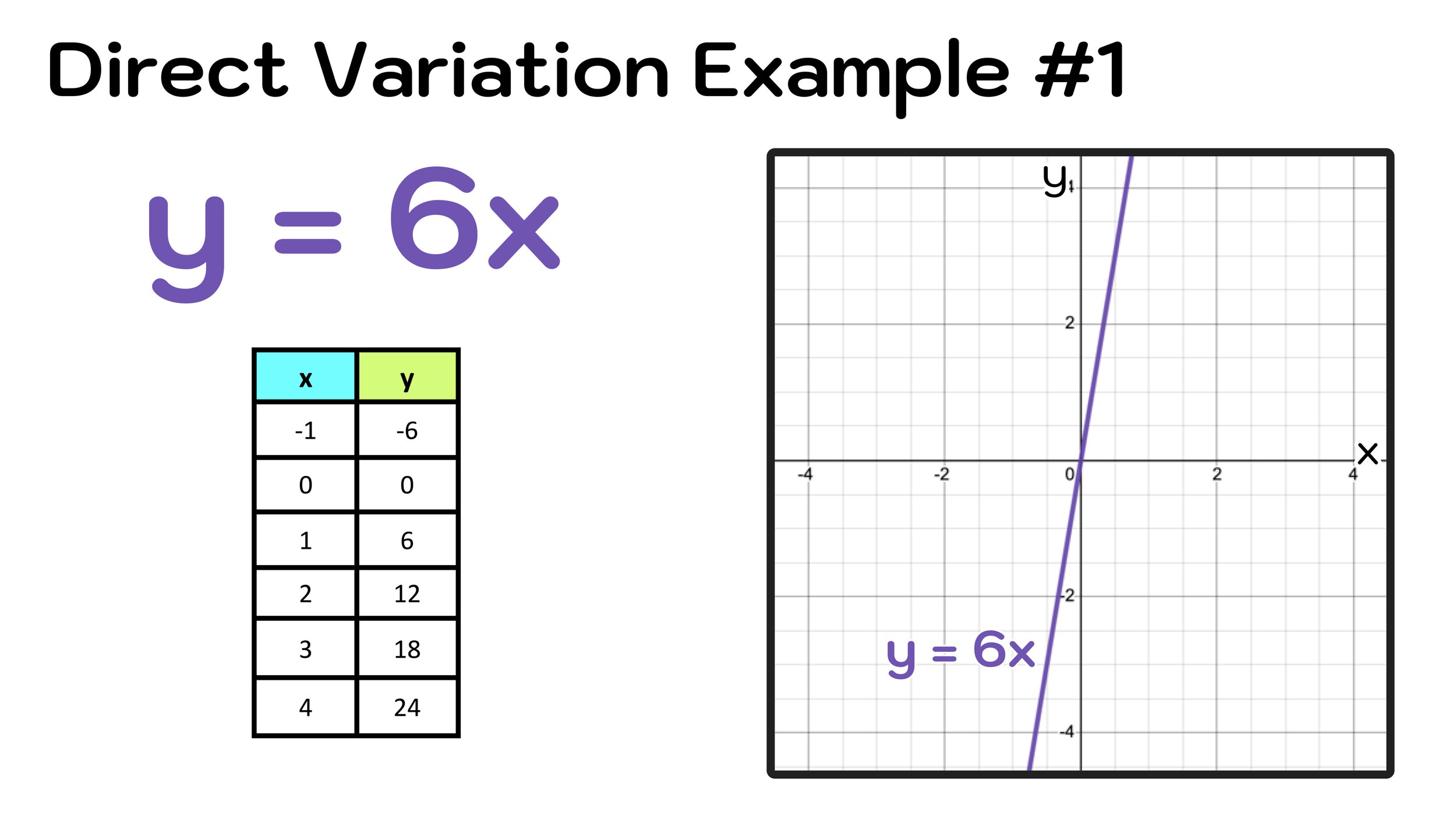
When you graph a direct variation equation, you’ll always get a straight line that passes through the origin, or the point (0,0). This happens because when one variable is zero, the other is too. For example, if you have the equation y = 2x, the graph will be a line that starts at the origin and slopes upward. The slope of the line is determined by the constant of proportionality, k.
Graphing direct variation is a great way to visualize how the two variables are related. It helps you see at a glance how much y changes for every unit of x. Plus, it’s a useful tool for solving problems and making predictions. So, next time you’re working with direct variation, don’t forget to sketch out the graph—it could make things a lot clearer.
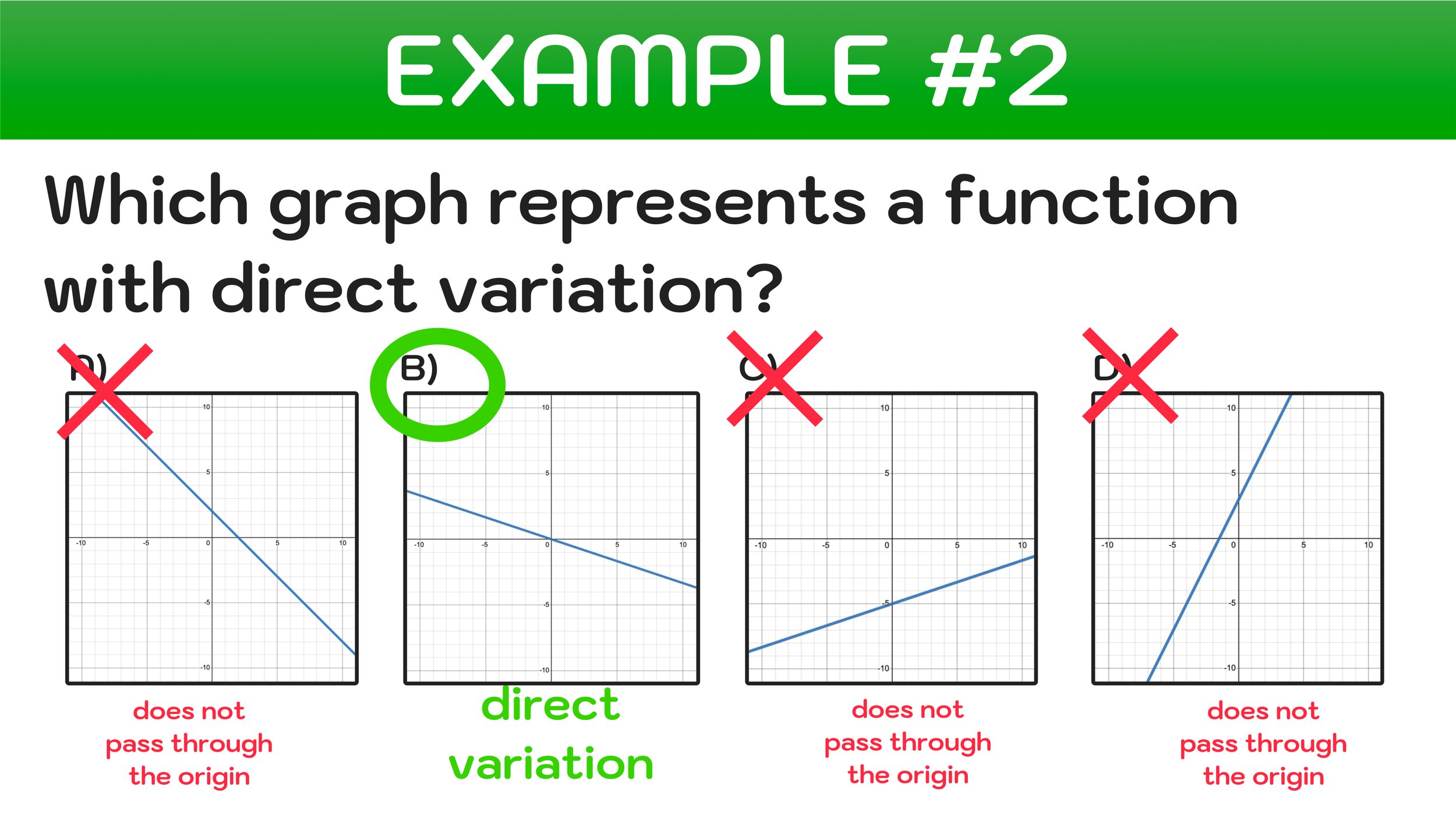
Is Direct Variation Always a Straight Line?
Yes, direct variation always results in a straight line when graphed. This is because the relationship between the two variables is linear. The constant of proportionality, k, determines the slope of the line, and the line always passes through the origin. However, it’s worth noting that not all linear relationships are direct variations. For example, a line that doesn’t pass through the origin isn’t a direct variation.
So, how do you know if a graph represents a direct variation? Look for a straight line that goes through the origin. If it does, you’re dealing with a direct variation. If not, it might be some other kind of relationship. This distinction is important when you’re analyzing data or solving problems involving linear equations.
How Can You Solve Direct Variation Problems?
Solving direct variation problems is all about using the formula y = kx. First, identify the two variables and the constant of proportionality. Then, plug the numbers into the formula and solve for the unknown. For example, if you know that y = 3x and x = 4, you can find y by multiplying 3 by 4, which gives you 12.
Sometimes, you might need to find the constant of proportionality first. For instance, if you’re told that y = 15 when x = 5, you can find k by dividing y by x. In this case, k would be 3. Once you have k, you can use it to solve for other values of y or x. It’s a straightforward process, but it requires a bit of practice to get the hang of it.
Can You Solve Direct Variation Problems Without a Formula?
While the formula y = kx is the most common way to solve direct variation problems, you can also use reasoning and logic. For example, if you know that doubling one variable doubles the other, you can make educated guesses about the relationship between them. However, using the formula is usually faster and more accurate, especially when dealing with larger numbers or more complex situations.
That said, it’s always good to have multiple tools in your problem-solving toolbox. Sometimes, thinking through a problem without relying on formulas can give you a deeper understanding of the underlying concepts. So, don’t be afraid to experiment with different approaches—just make sure you’re confident in your results.
Wrapping Up - What Have We Learned About Direct Variation?
Direct variation is a simple yet powerful concept that helps us understand how two things are connected. Whether you’re calculating costs, predicting outcomes, or just trying to make sense of the world, this idea is incredibly useful. We’ve looked at what direct variation is, how to write its equation, and how to graph it. We’ve also explored real-life examples and problem-solving techniques.
At the end of the day, direct variation is all about relationships. It’s about how one thing changes in response to another, and how we can use that knowledge to make predictions and solve problems. By now, you should have a pretty good grasp of how it works and why it matters. So, go out there and start spotting examples of direct variation in your own life—you might be surprised at how often it comes up!

Detail Author:
- Name : Ms. Amanda Medhurst Sr.
- Username : torrance73
- Email : easton.hoeger@wisozk.net
- Birthdate : 2002-02-16
- Address : 54214 Pollich Mountain Apt. 136 Jakaylaview, MD 92252-5353
- Phone : +1-260-899-0306
- Company : McClure, Monahan and D'Amore
- Job : Electromechanical Equipment Assembler
- Bio : Dolores quia est quas iure. Iste magni quas voluptatum voluptatem. Non voluptatem quisquam veritatis quod qui. Quia totam ut qui molestiae impedit non dolorem.
Socials
twitter:
- url : https://twitter.com/opal5428
- username : opal5428
- bio : Et ut ut minima quod quod. Voluptatem sed occaecati ut consequatur. Est qui et eos ut officia perspiciatis quia aperiam.
- followers : 6205
- following : 2227
instagram:
- url : https://instagram.com/cummerata2005
- username : cummerata2005
- bio : Minus vitae asperiores quam similique quisquam in sunt. Unde qui maiores quas blanditiis.
- followers : 786
- following : 2963
linkedin:
- url : https://linkedin.com/in/opal_dev
- username : opal_dev
- bio : Impedit laborum aut itaque non ut.
- followers : 4013
- following : 2194