Ever wondered what a coefficient really means? Whether you're diving into math, physics, or chemistry, you'll encounter this term sooner or later. In its simplest form, a coefficient is a number that multiplies a variable in an equation. Yet, it’s so much more than just a number. It plays a crucial role in various calculations, from balancing equations in chemistry to solving linear equations in math. Understanding coefficient meaning can open up a world of possibilities in both academic and real-world scenarios.
From its humble beginnings in the mid-17th century, the concept of coefficients has grown to become an essential part of mathematical and scientific studies. The word itself hints at a collaborative effort, suggesting the idea of factors working together to produce a result. This collaboration extends beyond math and science, finding applications in statistics, engineering, and even economics. Let's explore how this seemingly simple concept can have such a profound impact.
Whether you're a student trying to grasp algebraic expressions or a professional dealing with complex equations, knowing coefficient meaning can make all the difference. It's not just about memorizing definitions but truly understanding how coefficients interact with variables and constants. So, let's take a closer look at what makes coefficients so important and how they're used in different contexts.
Here's a quick overview of what we'll cover:
- Coefficient Meaning - What Exactly is a Coefficient?
- How Are Coefficients Used in Math?
- What Are the Different Types of Coefficients?
- Why Do Coefficients Matter in Algebra?
- Can Coefficients Help Solve Real-World Problems?
- How Do Coefficients Work in Statistics?
- What Does Coefficient Meaning Look Like in Chemistry?
- Final Thoughts - Summing Up Coefficient Importance
What Exactly is a Coefficient?
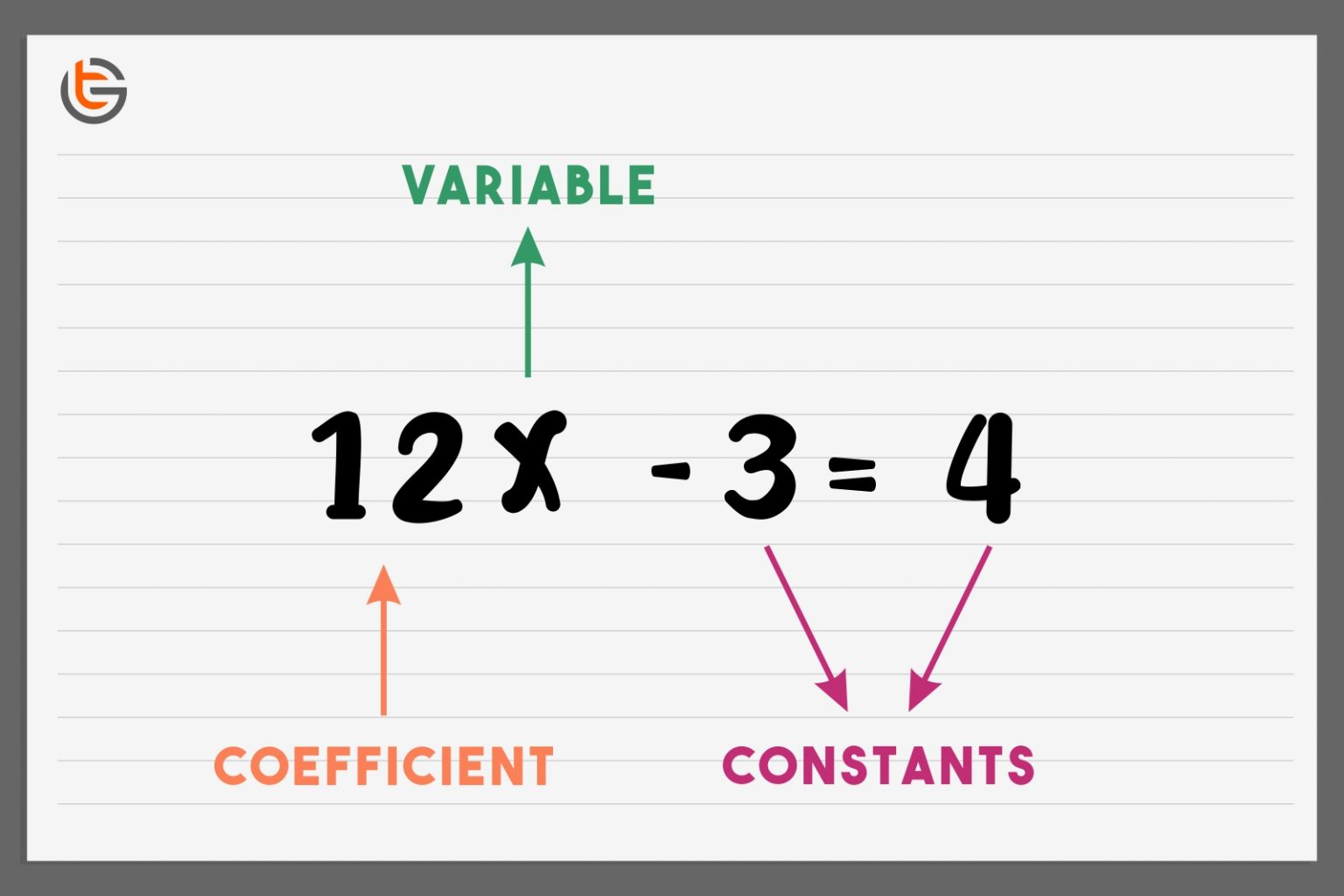
Alright, so what exactly is a coefficient? It's more than just a fancy word thrown around in math class. Think of it as a helper number that works alongside variables in equations. A coefficient tells us how many times a variable is being multiplied. For example, in the term 5x, the coefficient is 5, meaning 5 times x. It’s like a tag that sticks to a variable, guiding us on how to handle it in calculations.
Let’s break it down a bit more. Coefficients can be positive, negative, or even fractions. If you see -3y, the coefficient is -3, indicating that y is being multiplied by negative three. Similarly, in the term 1/2z, the coefficient is 1/2. Interestingly, if a variable appears without a number, like x, the coefficient is assumed to be 1. It’s almost like saying, "one times x." This little detail can save a lot of confusion when solving equations.
How Are Coefficients Used in Math?
Now that we’ve got the basics down, let’s talk about how coefficients are used in math. They’re not just random numbers; they’re part of a system that helps us solve problems. In algebraic expressions, coefficients guide us in simplifying terms and finding solutions. For instance, if you have the expression 3x + 2y, the coefficients 3 and 2 tell us how many times x and y are being multiplied, respectively.
So, why do we care so much about these numbers? Well, they’re like the glue that holds equations together. Without them, we’d have a hard time making sense of variables and constants. Coefficients help us organize information and make calculations more manageable. They’re especially useful in linear equations, where variables have an exponent of 1. It’s kind of like having a roadmap to navigate through complex problems.
What Are the Different Types of Coefficients?
Speaking of types, did you know there are different kinds of coefficients? Yep, they’re not all the same. Some coefficients are constants, meaning they don’t change. Others are variables themselves or can be letters instead of numbers. For example, in the term ax, a could be a constant or a variable depending on the context. This flexibility allows coefficients to adapt to various situations.
Let’s look at a few specific types. There’s the constant coefficient, which remains unchanged throughout a calculation. Then there’s the leading coefficient, found in polynomial expressions, which is the first number when terms are arranged in descending order. Parameter coefficients, on the other hand, are used to describe relatively stable characteristics of functions. These distinctions might seem small, but they make a big difference in how we approach problems.
Why Do Coefficients Matter in Algebra?
Alright, here’s the deal: coefficients matter a whole lot in algebra. They’re the building blocks of equations, helping us make sense of variables and constants. Without coefficients, algebra would be a lot harder to tackle. They provide clarity and structure, making it easier to solve problems and find solutions.
For example, when you’re solving a linear equation, coefficients guide you in isolating variables. They tell you exactly how much each variable contributes to the overall equation. This knowledge is invaluable when dealing with real-world scenarios, like calculating costs or predicting outcomes. Coefficients give us the tools to break down complex problems into simpler parts, making them much more approachable.
Can Coefficients Help Solve Real-World Problems?
Absolutely! Coefficients aren’t just for theoretical exercises; they have practical applications too. Imagine you’re trying to figure out how much paint you need for a room or how long it’ll take to fill a pool. Coefficients help you calculate these things by providing a framework for understanding relationships between variables. They’re like the secret ingredient that makes problem-solving possible.
In engineering, for instance, coefficients are used to measure friction or resistance. These values stay constant, allowing engineers to design safer and more efficient systems. Similarly, in economics, coefficients help model supply and demand, giving businesses insights into market trends. By understanding coefficient meaning, we can apply this knowledge to solve everyday challenges.
How Do Coefficients Work in Statistics?
Let’s shift gears a little and talk about statistics. In this field, coefficients take on a slightly different role. One common example is the coefficient of variation, which compares the standard deviation to the arithmetic mean. This ratio gives us a sense of how much variability exists in a dataset. It’s a handy tool for analyzing data and making informed decisions.
Another example is the correlation coefficient, which measures the strength and direction of a relationship between two variables. This type of coefficient helps statisticians identify patterns and trends, leading to better predictions and insights. Whether you’re analyzing stock prices or customer behavior, coefficients provide the data you need to make sense of it all.
What Does Coefficient Meaning Look Like in Chemistry?
Finally, let’s explore how coefficients are used in chemistry. In chemical equations, coefficients balance the number of atoms on each side of the equation. This ensures that matter is neither created nor destroyed during a reaction, adhering to the law of conservation. For instance, in the reaction 2H₂ + O₂ → 2H₂O, the coefficients 2 and 1 tell us how many molecules of hydrogen and oxygen are involved.
Chemists rely on coefficients to ensure accurate measurements and precise calculations. They help determine the correct proportions of reactants needed for a reaction, preventing waste and ensuring safety. By understanding coefficient meaning in chemistry, scientists can create more effective experiments and develop innovative solutions to real-world problems.
Final Thoughts - Summing Up Coefficient Importance
So, there you have it – a closer look at coefficient meaning and why it matters. Whether you’re working with math, physics, chemistry, or statistics, coefficients play a vital role in helping us understand and solve problems. They provide structure, clarity, and insight, making complex calculations more manageable. By learning how coefficients work, we can unlock new ways of thinking and problem-solving, both in academics and in everyday life.


Detail Author:
- Name : Prof. Domenick Senger
- Username : kristin09
- Email : marcus.macejkovic@yahoo.com
- Birthdate : 1994-04-17
- Address : 51944 Lesch Mill Apt. 981 Port Kamille, AL 93093
- Phone : 1-603-245-4707
- Company : Rosenbaum Ltd
- Job : Mechanical Engineer
- Bio : Ad sit dolore est nihil ut numquam nam facilis. Commodi veritatis in iste soluta eius laudantium illo. Cupiditate beatae nemo qui voluptas assumenda voluptatem.
Socials
twitter:
- url : https://twitter.com/glenferry
- username : glenferry
- bio : Temporibus eos aut ullam id adipisci sed omnis. Tempora dolores eos rem autem. Velit accusamus error qui. Sit ut nulla dolorem laborum.
- followers : 2754
- following : 821
tiktok:
- url : https://tiktok.com/@glen_ferry
- username : glen_ferry
- bio : Voluptates corporis illum accusantium laborum est.
- followers : 3953
- following : 2993
instagram:
- url : https://instagram.com/glen_ferry
- username : glen_ferry
- bio : Aut et omnis cumque asperiores enim. Sint sit suscipit unde exercitationem rerum.
- followers : 1971
- following : 1290
facebook:
- url : https://facebook.com/glenferry
- username : glenferry
- bio : Et nobis vero possimus provident sit culpa ea.
- followers : 6717
- following : 1625