Congruent Definition - What It Really Means In Geometry And Beyond

## Table of Contents

What Is Congruence?
How to Prove Triangles Are Congruent?
Why Is Congruent Definition Important?
Can Congruent Figures Differ in Orientation?
Examples of Congruuent Shapes
How Does Congruence Relate to Algebra?
Does the Congruent Definition Apply to Trigonometry?
Final Thoughts

Congruent definition is a term that comes up often in math, but what exactly does it mean? If you’re just starting out in geometry or need a refresher, congruence refers to shapes that are identical in both size and form. Think of it like this: if you take two objects and they fit perfectly on top of each other without any gaps or overlaps, they’re congruent. It’s more than just being similar; it’s about matching every detail. This concept applies across many areas of mathematics, so let’s explore what makes congruence so important.

Understanding congruence isn’t just for geometry buffs. It has practical applications in everyday life, from designing patterns to ensuring structures are stable. For instance, when architects design buildings, they rely on congruence to ensure that parts fit together correctly. Similarly, engineers use congruence principles to ensure machinery components align properly. In fact, congruence plays a role in everything from art to science, making it a foundational concept worth exploring.

Before diving deeper, it’s worth noting that congruence isn’t limited to geometry alone. You’ll find it popping up in algebra and trigonometry as well. These branches of math use congruence to establish relationships between numbers and shapes. So, if you’re curious about how congruence works in different contexts, you’re in the right place. Let’s break it down step by step, starting with the basics.

What Is Congruence?

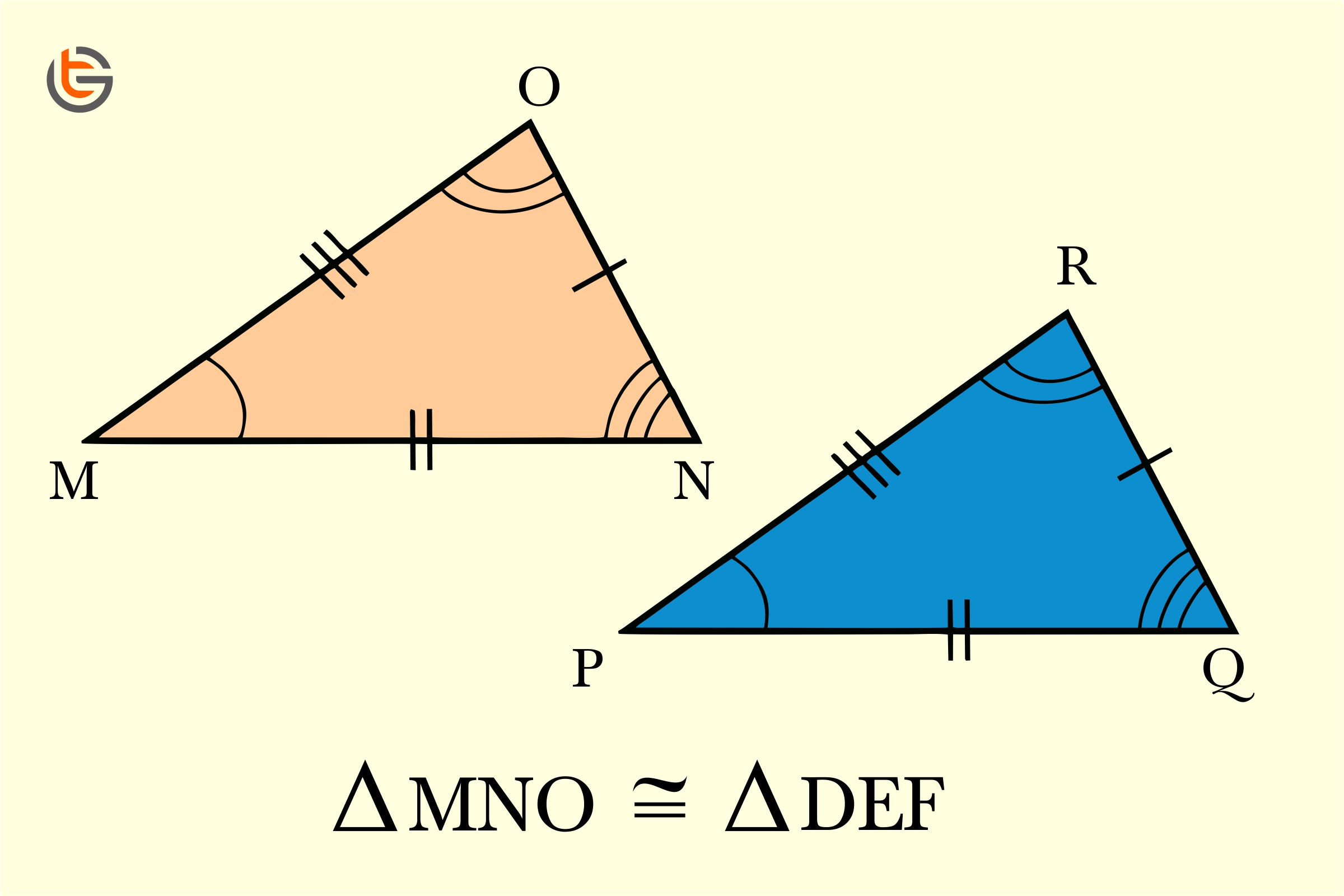
So, what exactly does it mean for two shapes to be congruent? Simply put, congruence happens when two figures have the exact same size and shape. For example, two squares with the same side lengths or two circles with the same radius are congruent. The idea is that if you were to place one shape on top of the other, they would line up perfectly. This isn’t just about appearance; it’s about measurable properties like angles and sides matching exactly.

Now, here’s a little trick to test congruence: try flipping, rotating, or sliding one shape to see if it matches another. If they line up perfectly after these transformations, they’re congruent. This concept is especially useful in geometry, where proving congruence is often part of solving problems. It’s not just about shapes, though—congruence applies to angles, line segments, and even entire figures.

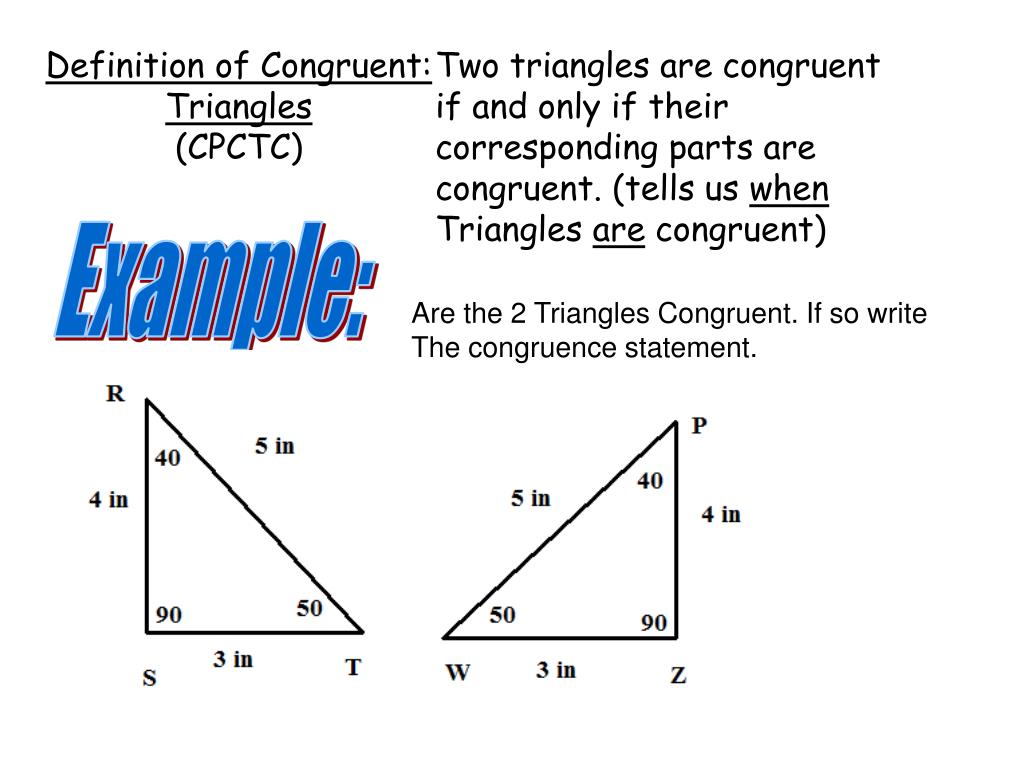
How to Prove Triangles Are Congruent?

Triangles are a great example to explore congruence because there are specific rules to prove they’re congruent. For instance, the Side-Side-Side (SSS) rule states that if all three sides of one triangle match the sides of another, they’re congruent. Similarly, the Angle-Side-Angle (ASA) rule says that if two angles and the included side match, the triangles are congruent. There’s also Side-Angle-Side (SAS) and Hypotenuse-Leg (HL) for right triangles.

These methods make it easier to determine congruence without having to measure every single part of the triangles. Think of them as shortcuts that mathematicians use to save time and effort. By the way, these rules aren’t just theoretical; they’re practical tools that help solve real-world problems, like calculating distances or designing symmetrical objects.

Why Is Congruent Definition Important?

Alright, so why does congruence matter in math? Well, it’s more than just a fancy word. Congruence helps us understand how shapes relate to each other. For example, if two triangles are congruent, we know their corresponding angles and sides are equal. This knowledge is crucial for proving theorems and solving geometric problems. It’s like having a universal language that lets us compare and contrast shapes easily.

In some respects, congruence acts as a bridge between different areas of math. It connects geometry with algebra and trigonometry, creating a more unified understanding of mathematical principles. Plus, it’s not just about solving equations—it’s about seeing patterns and making connections. So, whether you’re working on a complex proof or designing a simple pattern, congruence gives you the tools you need to succeed.

Can Congruent Figures Differ in Orientation?

That’s a great question! Yes, congruent figures can have different orientations. For example, imagine a triangle pointing upward and another pointing downward. If all their sides and angles match, they’re still considered congruent. The key is that their measurements remain identical, even if their positions or directions change. It’s kind of like looking at a mirror image—everything is the same, just flipped around.

This idea is important because it shows that congruence isn’t limited by how something looks on the surface. Instead, it focuses on the underlying properties that define a shape. So, if you’re working with congruent figures, don’t get thrown off by their orientation. As long as the measurements check out, you’re good to go.

Examples of Congruent Shapes

Let’s take a look at some examples to make this clearer. Picture two rectangles with the exact same length and width. They’re congruent because they share the same dimensions, regardless of their orientation. Another example is two circles with the same radius—they’re congruent because their sizes are identical. Even line segments can be congruent if they have the same length.

Now, here’s where it gets interesting. Sometimes, shapes might look similar but aren’t actually congruent. For instance, two triangles might have the same angles but different side lengths. In that case, they’re similar, not congruent. This distinction is important because it affects how we approach problems and interpret results. So, always double-check those measurements before labeling something as congruent.

How Does Congruence Relate to Algebra?

In algebra, congruence takes on a slightly different meaning. It’s used to describe numbers that have the same remainder when divided by a specific value. For example, if you divide 10 and 15 by 5, both leave a remainder of 0. In this case, we say that 10 and 15 are congruent modulo 5. This concept is useful in number theory and cryptography, where patterns in numbers play a big role.

It’s worth noting that algebraic congruence doesn’t deal with shapes or sizes. Instead, it focuses on numerical relationships. Still, the idea of matching properties remains consistent. Whether you’re working with geometric figures or algebraic equations, congruence is all about finding similarities and making connections.

Does the Congruent Definition Apply to Trigonometry?

Absolutely! In trigonometry, congruence is used to describe triangles that have the same size and shape. This is particularly useful when solving problems involving angles and side lengths. For example, if you know two triangles are congruent, you can use that information to calculate unknown values. It’s like having a built-in shortcut that simplifies complex calculations.

Trigonometry often relies on congruence to establish relationships between angles and sides. By identifying congruent triangles, you can apply formulas and theorems to solve problems more efficiently. This is especially helpful in fields like engineering and physics, where precise measurements are critical.

Final Thoughts

So, what have we learned about congruence? To sum it up, congruence is about identifying shapes, figures, or numbers that match perfectly in size and form. Whether you’re working with triangles, circles, or algebraic equations, congruence provides a framework for understanding relationships and solving problems. It’s a powerful tool that connects different areas of math and helps us make sense of the world around us.

Remember, congruence isn’t just about memorizing rules or definitions. It’s about seeing patterns, making connections, and applying what you’ve learned to real-life situations. So, the next time you encounter congruence in math, take a moment to appreciate its significance. After all, it’s more than just a concept—it’s a key to unlocking deeper mathematical insights.

PPT - Triangle Congruence PowerPoint Presentation, free download - ID

Details

PPT - 2.2a: Exploring Congruent Triangles PowerPoint Presentation, free

Details

Details

Detail Author:

Name : Lia Hand
Username : miracle09
Email : eichmann.domingo@mcglynn.com
Birthdate : 2005-05-13
Address : 3504 Alek Row West Ryleychester, AR 49127-5913
Phone : +1-859-653-4332
Company : Funk Group
Job : Appliance Repairer
Bio : At et harum ad et impedit est. Autem soluta omnis excepturi corrupti. Et assumenda quidem dolores perspiciatis dolorum.

Socials

facebook:

url : https://facebook.com/ronnyparisian
username : ronnyparisian
bio : Sint corrupti expedita eligendi earum adipisci asperiores dignissimos.
followers : 5445
following : 2433